When I'm not flying airplanes, riding my bike or helping to raise my grandson, I am teaching math, art and a little science to school aged children. Once in a while we get caught up in a flight theme where we talk about airplanes, birds, aeronautical terms and experiments. One of my favorites has always been folding and stapling a sheet of paper into an airfoil and then talking about how wings fly using Bernoulli's Law. We blow on the leading edge of the paper airfoil and I explain how the air on top has to move faster than the air on the bottom so that both halves will meet at the end of the airfoil at the same time. This provides the wing with "lift."
After that explanation I always feel warm and fuzzy thinking I had passed on the important information all young people should know as they enter the adult world. I believe aeronautics should be part of one's upbringing as is math, reading, writing, music and art." I felt happy that I had done my part by bringing my students state-of-the-art information about flying.
After all I flew airplanes, I should know!
Then ... a parent of one my students wrote this email.
Hi Alice,
Anna's mom Carolyn here :). I've been trying to understand Bernoulli's principle a bit more because I just didn't get it on Tuesday and I found this website. It's fascinating, and I'm trying to work my way through it...what do you think? Seems they raise some good points...
http://www.aa.washington.edu/faculty/eberhardt/lift.htm
Just thought I'd share it with you--
see you next week :)
Carolyn
It sounded so simple, unthreatening and sweet, so, of course, I went to the web site (which has moved to http://home.comcast.net/%7Eclipper-108/lift.htm, and proceeded to have my mind completely and utterly blown away by David Anderson, Firmi National Accelerator Laboratory Re. dfa180@aol.com and Scott Eberhardt, Dept. of Aeronauttics and Astronautics University of Washington, Seattle, WA 91895-2400, scott@aa.washington.edu who wrote "A Physical Description of Flight."
In this article the author's note that the popular description of lift was indeed the one I had been teaching and it goes something like this:
"Students of physics and aerodynamics are taught that an airplane flies as a result of the Bernoulli principle, which says that if air speeds up the pressure is lowered. (In fact this is not always true. The air flows fast over the airplane's static port but the altimeter still reads the correct altitude.) The argument goes that a wing has lift because the air goes faster over the top creating a region of low pressure. This explanation usually satisfies the curious and few challenge the conclusions. Some may wonder why the air goes faster over the top of the wing and this is where the popular explanation of lift falls apart.
But, who says the separated air must meet at the trailing edge at the same time? Figure 1 shows the airflow over a wing in a simulated wind tunnel. In the simulation, smoke is introduced periodically. One can see that the air that goes over the top of the wing gets to the trailing edge considerably before the air that goes under the wing. In fact, the air is accelerated much faster than would be predicted by equal transit times. Also, on close inspection one sees that the air going under the wing is slowed down from the "free-stream" velocity of the air. The principle of equal transit times holds only for a wing with zero lift.
Above is a picture of a simulation of the airflow over a wing in a wind tunnel, with "smoke".
The popular explanation also implies that inverted flight is impossible. It certainly does not address acrobatic airplanes, with symmetric wings (the top and bottom surfaces are the same shape), or how a wing adjusts for the great changes in load such as when pulling out of a dive or in a steep turn.
So, why has the popular explanation prevailed for so long? One answer is that the Bernoulli principle is easy to understand. There is nothing wrong with the Bernoulli principle, or with the statement that the air goes faster over the top of the wing. But, as the above discussion suggests, our understanding is not complete with this explanation. The problem is that we are missing a vital piece when we apply Bernoulli's principle. We can calculate the pressures around the wing if we know the speed of the air over and under the wing, but how do we determine the speed? As we will soon see, the air accelerates over the wing because the pressure is lower, not the other way around.
Another fundamental shortcoming of the popular explanation is that it ignores the work that is done. Lift requires power (which is work per time). As will be seen later, an understanding of power is key to the understanding of many of the interesting phenomena of lift."
Following this the authors proceed to explain another perspective, perhaps a truer one about lift.
"So, how does a wing generate lift? To begin to understand lift we must review Newton's first and third laws. (We will introduce Newton's second law a little later.) Newton's first law states a body at rest will remain at rest, or a body in motion will continue in straight-line motion unless subjected to an external applied force. That means, if one sees a bend in the flow of air, or if air originally at rest is accelerated into motion, a force is acting on it. Newton's third law states that for every action there is an equal and opposite reaction. As an example, an object sitting on a table exerts a force on the table (its weight) and the table puts an equal and opposite force on the object to hold it up. In order to generate lift a wing must do something to the air. What the wing does to the air is the action while lift is the reaction."
We are then asked to compare the two figures above that show streamlines over a wing. In the first figure, the air comes straight at the wing, bends around it, and then leaves straight behind the wing. "We have all seen similar pictures, even in flight manuals. But, the air leaves the wing exactly as it appeared ahead of the wing. There is no net action on the air so there can be no lift! The second lower figure shows the streamlines, as they should be drawn. The air passes over the wing and is bent down. Newton's first law says that them must be a force on the air to bend it down (the action). Newton's third law says that there must be an equal and opposite force (up) on the wing (the reaction). To generate lift a wing must divert lots of air down."
At this point I wrote to one of my most respected and favorite engineers regarding all of this, Howard Rush.
Hi Howard,
I don't know if I can ask you this question as politely as you asked me once before, but here goes.
I am teaching some physics about flight and Bernoulli's Principle has come up. There has been some discussion about how this principle doesn't really explain lift and that there are other factors involved. This website was referred to me and there is an interesting discussion about lift. I would like to know your opinion on the whole lift thing and how do we explain inverted flight if the airfoil is upside down?
What do you think? I ask of a person whose engineering knowledge I most respect.
Respectfully yours, Alice Cotton-Royer ( - :
Here is what he said:
Ms. Alice,
The Web site is correct, but there is a story here. 70 years or so ago, a nontechnical person asked Theodor Von Karman (I think) how wings worked. Von Karman, who knew better, made up the nonsense about the flow going over the top and bottom of the wing and meeting at the trailing edge at the same time. When one of his colleagues asked why he made up such bullshit, Von Karman is reported to have said, "When you are speaking to technically illiterate people you must resort to the plausible falsehood instead of the difficult truth." It probably doesn't make much difference how people think a wing works except for the few dozen people in the world actually doing basic aerodynamics. The equal-transit-time story caught on, though, and aerodynamicists ever since have wanted to wring the originator's neck and go to a lot of bother to refute the story. There's no scientific debate about how wings work.
I think I'd show the students the whole Web page if they've heard the equal-transit-time explanation and are confused. If they haven't heard that explanation, just omit the introduction and "The popular description of lift" section.
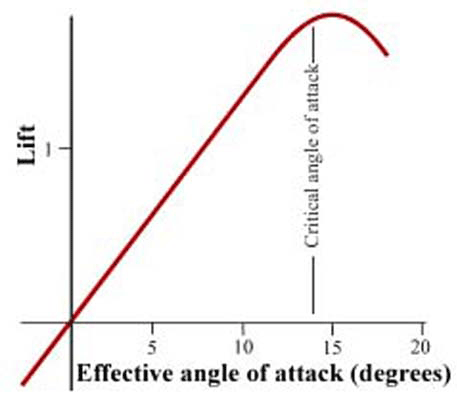
Figure 8 (the figure above) of the Web site shows lift vs. angle of attack for a symmetrical airfoil. To fly level, you put in a little up elevator to hold the wing at the angle of attack that gives just enough lift to balance the airplane's weight. If you put in some more up elevator, the airplane will do an inside loop. Enough up elevator to push the angle of attack near what Figure 8 calls the "critical angle of attack" will give an inside square corner. For a symmetrical airfoil, the red line of Figure 8 continues for negative angle of attack and has the same shape as for positive angle of attack. I forget what you call that kind of symmetry, but if angle of attack A gives lift B, angle of attack -A gives lift -B. So to fly level upside down, you'd put in enough negative angle of attack to give just enough lift to balance the airplane's weight. Wings with airfoils that aren't symmetrical can fly upside down, too, but the "critical angle of attack" on the negative side will be closer to the y axis, and the airplane can't make as much lift upside down as right side up. Hence, an airplane with an airfoil with more curve on the top than on the bottom can turn tighter inside loops than outside loops.
Marilou's nephew in Nebraska asked the same question. I sent him a copy of Understanding Flight, the book cited at the top of this Web site. I know Scott Eberhardt, one of the authors. He is a really cool guy.
I hope to see you in Salem for the Follies,
Howard
Well that did it. But before I could leave this topic and prepare my new lesson plans I needed to know about Theodore von Karman.
Theodore von Kármán (May 11, 1881 May 6, 1963)
was a Hungarian-American engineer and physicist who was active primarily
in the fields of aeronautics.
He was one of the few true
giants of aeronautics that could compete with the great minds of the twentieth
century. A genius by all accounts, he made fundamental contributions to
the theory and practice of aerodynamics and related technologies. He was
personally responsible for many key advances in aerodynamics, notably his
work on supersonic and hypersonic airflow characterization.
Kármán's fame was in the use of mathematical tools to study fluid flow, and the interpretation of those results to guide practical designs. He was instrumental in recognizing the importance of the swept-back wings that are ubiquitous in modern jet aircraft. Von Kármán died in 1963. Craters on Mars and the Moon are named in his honor. University of Southern California Professor Shirley Thomas (after nearly two decades of petitioning) was able to create a postage stamp in his honor[1]. It was first issued in 1992.
If you should care to read the rest of the "A Physical Description of Flight" article at http://www.aa.washington.edu/faculty/eberhardt/lift.htm that used to be http://www.aa.washington.edu/faculty/eberhardt/lift.htm
The authors will talk about the Coanda effect, downwash, lift as a function of angle of attack, the wing as "air scoop", lift requires power, wing efficiency, power and wing loading, wing vortices and ground effect.
Enjoy!
This page was updated June 9, 2007